波士顿房价数据集的处理

需求

波士顿房价数据集在scikit-learn1.2版本以后被移除了。目前自己用的刚好是1.2版本，但是需要复现书中的一些代码（Python机器学习基础教程），所以需要从其他途径获取波士顿房价数据集，主要是获得data(506, 104)和相关的target。

实现

1、获得data(506,104)：

import numpy as np
import pandas as pd
data_url = "http://lib.stat.cmu.edu/datasets/boston"
raw_df = pd.read_csv(data_url, sep="\s+", skiprows=22, header=None)
data = np.hstack([raw_df.values[::2, :], raw_df.values[1::2, :2]])
target = raw_df.values[1::2, 2] # 归一化和特征构造后都没有变化
print("Data shape: {}".format(data.shape))

X = MinMaxScaler().fit_transform(data)
X = PolynomialFeatures(degree=2, include_bias=False).fit_transform(X) # X即为最后的data(506,104)
print(X.shape)

# out:
# Data shape: (506, 13)  
# X shape: (506, 104)

2、获取target：

对数据进行归一化和多项式构造，并没有改变行的布局，只是列发生变化，所以shape变化的前后，target不变。

理解

特征的由少变多

最初的 13 个特征加上这 13 个特征两两组合（有放回）得到的 91 个特征，一共有 104 个特征。

两两组合计算：思路1：

共13个特征，第一次抽取1这个特征，再放回1，也就是1可以和13个特征组合，也就是允许1和1组合。

第二次抽取2这个特征，再放回2，2也可以和13个特征组合，但是第一次抽取时1和2已经组合过了，所以需要去除这个1和2组合，即2只能和12个特征组合。

第三次抽取3这个特征，再放回3，3也可以和13个特征组合，但是第一次3和1已经组合过了，第二次3和2已经组合过了，即3只能和11个特征组合。

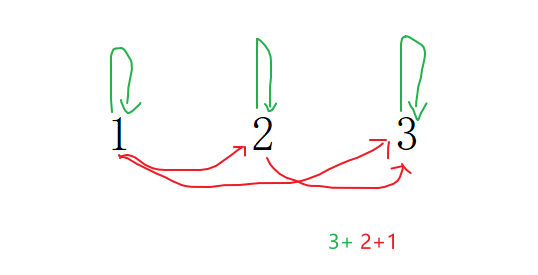
第 1 个特征可以与 13 个特征相乘，第 2 个可以与 12 个特征相乘（除了第 1 个），第 3 个可以与 11 个特征相乘……依次相加，13 + 12 + 11 + … + 1 = 91。

思路2：当成两部分计算，之前自己算成78，就是忽略了有放回这个条件即忽略了绿色部分；

MinMaxScaler()

Feature scaling，常见的提法有“特征归一化”、“标准化”，是数据预处理中的重要技术。^[3]本文将Feature scaling叫作特征标准化，归一化指代min-max normalization。

常用feature scaling（标准化）方法：

Rescaling (min-max normalization、range scaling) / 归一化
Mean normalization
Standardization (Z-score Normalization)
Scaling to unit length

上述4种feature scaling方式，前3种为逐行操作，最后1种为逐列操作。本文只讨论min-max normalization这个方式。

当数据(x)按照最小值中心化后，再按极差（最大值 - 最小值）缩放，数据移动了最小值个单位，并且会被收敛到 [0,1] 之间(默认)，而这个过程，就叫做数据归一化(Normalization，又称Min-Max Scaling)^[1]。

归一化其实就是标准化的一种方式，只不过归一化是将数据映射到了[0,1]这个区间中。^[2]

归一化之后的数据服从正态分布，公式如下： \[X^* = \frac{x-min(x)}{max(x)-min(x)}\]

preprocessing.MinMaxScaler 官方文档

1	class sklearn.preprocessing.MinMaxScaler(feature_range=(0, 1), *, copy=True, clip=False)

默认数据归一到 [ 0，1 ]

from sklearn.preprocessing import MinMaxScaler
data = np.array([3,4,5]).reshape(-1, 1) 
mm = MinMaxScaler()   # 实例化
mm_data = mm.fit_transform(data)  #与下面注释的两行一样
# mm = mm.fit(data)  # fit，在这里本质是生成min(x)和max(x)
# mm_data = mm.transform(data) # 通过接口导出结果

print("data：\n{}\n".format(data))
print("归一化的data：\n{}".format(mm_data))

# out：
# data：
# [[3]
#  [4]
#  [5]]

# 归一化的data：
# [[0. ]
#  [0.5]
#  [1. ]]

data = np.array([[3,4,5],[1,78,3],[60,56,32],[97,43,12]])
mm = MinMaxScaler()  
mm_data = mm.fit_transform(data)

print("data：\n{}\n".format(data))
print("归一化的data：\n{}\n".format(mm_data))
print("data的shape:{}".format(data.shape))
print("最大值：{}".format(mm.data_max_))
print("最小值：{}".format(mm.data_min_))

# out:
# data：
# [[ 3  4  5]
#  [ 1 78  3]
#  [60 56 32]
#  [97 43 12]]

# 归一化的data：
# [[0.02083333 0.         0.06896552]
#  [0.         1.         0.        ]
#  [0.61458333 0.7027027  1.        ]
#  [1.         0.52702703 0.31034483]]

# data的shape:(4, 3)
# 最大值：[97. 78. 32.]
# 最小值：[1. 4. 3.]

列是特征，行是样本，所以这里的归一化都是以列为单位；

import numpy as np
import pandas as pd
from sklearn.preprocessing import MinMaxScaler, PolynomialFeatures

np.set_printoptions(threshold = np.inf) # 不使用省略号表示
np.set_printoptions(suppress = True) # 不使用科学计数显示

data_url = "http://lib.stat.cmu.edu/datasets/boston"
raw_df = pd.read_csv(data_url, sep="\s+", skiprows=22, header=None)
data = np.hstack([raw_df.values[::2, :], raw_df.values[1::2, :2]])
target = raw_df.values[1::2, 2]

mm = MinMaxScaler()  # 实例化
mm = mm.fit(data)   # 得出最大值，最小值
data_g = mm.transform(data) # 导出归一化结果

print("data shape: {}".format(data.shape))
print("X shape: {}\n".format(data_g.shape)) # 只做了归一化，前后特征维度没变

print("data前3行：\n{}\n".format(data[0:3,]))  # 验证按列进行归一化
print("归一化后的data_g:\n{}\n".format(data_g[0:3,]))
print("最小值：{}\n".format(mm.data_min_))
print("最大值：{}\n".format(mm.data_max_))

# out:
# data shape: (506, 13)
# X shape: (506, 13)

# data前3行：
# [[  0.00632  18.        2.31      0.        0.538     6.575    65.2
#     4.09      1.      296.       15.3     396.9       4.98   ]
#  [  0.02731   0.        7.07      0.        0.469     6.421    78.9
#     4.9671    2.      242.       17.8     396.9       9.14   ]
#  [  0.02729   0.        7.07      0.        0.469     7.185    61.1
#     4.9671    2.      242.       17.8     392.83      4.03   ]]

# 归一化后的data_g:
# [[0.         0.18       0.06781525 0.         0.31481481 0.57750527
#   0.64160659 0.26920314 0.         0.20801527 0.28723404 1.
#   0.08967991]
#  [0.00023592 0.         0.24230205 0.         0.17283951 0.5479977
#   0.78269825 0.34896198 0.04347826 0.10496183 0.55319149 1.
#   0.2044702 ]
#  [0.0002357  0.         0.24230205 0.         0.17283951 0.6943859
#   0.59938208 0.34896198 0.04347826 0.10496183 0.55319149 0.98973725
#   0.06346578]]

# 最小值：[  0.00632   0.        0.46      0.        0.385     3.561     2.9
#    1.1296    1.      187.       12.6       0.32      1.73   ]

# 最大值：[ 88.9762 100.      27.74     1.       0.871    8.78   100.      12.1265
#   24.     711.      22.     396.9     37.97  ]

print((0.00632-0.00632)/(88.9762-0.00632))
print((0.02731-0.00632)/(88.9762-0.00632))
print((0.02729-0.00632)/(88.9762-0.00632))

# out:
# 0.0
# 0.00023592253917842758
# 0.00023569774400055386

PolynomialFeatures()

再对波士顿数据进行归一化后，需要将13个特征两两相乘，添加更多的特征，需要用到多项式进行特征构造，即使用 PolynomialFeatures

PolynomialFeatures官方文档

使用 sklearn.preprocessing.PolynomialFeatures 这个类可以进行特征的构造，构造的方式就是特征与特征相乘（自己与自己，自己与其他人），这种方式叫做使用多项式的方式。例如：有 a、b 两个特征，那么它的 2 次多项式的次数为 \([1,a,b,a^{2},ab,b^{2}]\) ^[4]。

PolynomialFeatures 这个类有 3 个参数：

degree：控制多项式的次数；
interaction_only：默认为 False，如果指定为 True，那么就不会有特征自己和自己结合的项，组合的特征中没有 \(a^2\) 和 \(b^2\) ；
include_bias：默认为 True 。如果为 True 的话，那么结果中就会有 0 次幂项，即全为 1 这一列。

from sklearn.preprocessing import  PolynomialFeatures

x = np.array([[2,3],[4,5]])
poly = PolynomialFeatures(degree=2, include_bias=False) # 实例化，指定2次多项式，去除0次幂项
x_d = poly.fit_transform(x)  # 导出特征构造的结果

print("特征构造前：\n{}\n".format(x))
print("特征构造后：\n{}".format(x_d))

# out：
# 特征构造前：
# [[2 3]
#  [4 5]]

# 特征构造后：
# [[ 2.  3.  4.  6.  9.]
#  [ 4.  5. 16. 20. 25.]]

Jay's Blog

波士顿房价数据集的处理

需求

实现

理解

特征的由少变多

MinMaxScaler()

PolynomialFeatures()

参考文章