皮尔森（逊）相关系数（Pearson Correlation Coefficient, PCC）

摘要

\(R\) ：相关系数（correlation coefficient），即皮尔森相关系数，值位于 -1 到 1 之间，即负相关和正相关，绝对值越大表明相关性越强，P值越小越相关。

\(R^2\) ：决定系数（coefficient of determination），\(R^2\) 值越接近 1，吻合程度越高，越接近 0，则吻合程度越低。

决定系数 = 相关系数平方

皮尔森相关系数

皮尔森相关系数也称皮尔森积矩相关系数(Pearson product-moment correlation coefficient) ，是一种线性相关系数，是最常用的一种相关系数。记为 R，用来反映变量X和变量Y的线性相关程度，R 值介于-1到1之间，绝对值越大表明相关性越强。^[1]

适用连续变量。

相关系数与相关程度一般划分为

0.8 - 1.0 极强相关
0.6 - 0.8 强相关
0.4 - 0.6 中等程度相关
0.2 - 0.4 弱相关
0.0 - 0.2 极弱相关或无相关

原假设：两者不存在相关性 P值小，即我们观察的样本（不存在相关性）发生的概率小，存在相关性的概率大，如果原假设成立即不存在相关性，那么我们这个样本就很极端很显著。

相关系数绝对值越大，越相关，P值越小越相关。

scipy.stats.pearsonr(x, y, *, alternative='two-sided') ：^[2]

# Python实现
from scipy.stats import pearsonr

x = [1,2,3,4]
y = [1.2,2.2,3.1,4.1]
result = pearsonr(x,y)
print("pearson相关系数: {:.6f}".format(result.statistic))  # result[0]
print("P-Value: {:.6f}".format(result.pvalue))  # result[1]

# out:
# pearson相关系数: 0.999783
# P-Value: 0.000217

numpy.corrcoef(x, y=None, rowvar=True, bias=<no value>, ddof=<no value>, *, dtype=None)

Return Pearson product-moment correlation coefficients.^[5]

这里计算的是特征与特征（行与行/列与列）的相关系数。

import numpy as np
a = pd.Series([1,2,3,4,5,6,7,8,9,10])
b = pd.Series([2,4,1,5,1,3,6,2,7,0])
c = pd.Series([0,3,2,1,4,7,1,9,6,2])
x = np.vstack((a,b,c))
r = np.corrcoef(x)
print("x:\n{}\n".format(x))
print("r:\n{}".format(r))

# out:
# x:
# [[ 1  2  3  4  5  6  7  8  9 10]
#  [ 2  4  1  5  1  3  6  2  7  0]
#  [ 0  3  2  1  4  7  1  9  6  2]]

# r:
# [[1.         0.10233683 0.47840854]
#  [0.10233683 1.         0.0242104 ]
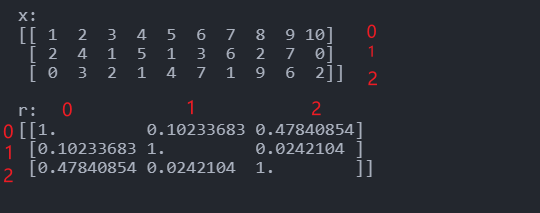
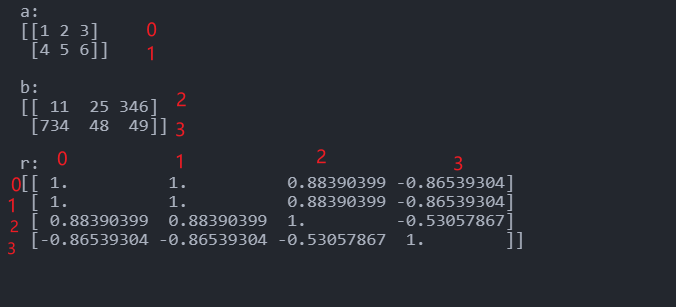
#  [0.47840854 0.0242104  1.        ]]

a = np.array([[1, 2, 3], [4, 5, 6]])
b = np.array([[11, 25, 346], [734, 48, 49]])
r = np.corrcoef(a,b)

print("a:\n{}\n".format(a))
print("b:\n{}\n".format(b))
print("r:\n{}\n".format(r))

# out:
# a:
# [[1 2 3]
#  [4 5 6]]

# b:
# [[ 11  25 346]
#  [734  48  49]]

# r:
# [[ 1.          1.          0.88390399 -0.86539304]
#  [ 1.          1.          0.88390399 -0.86539304]
#  [ 0.88390399  0.88390399  1.         -0.53057867]
#  [-0.86539304 -0.86539304 -0.53057867  1.        ]]

线性回归的R平方

线性回归后得到的 R 平方和使用皮尔森相关求得的 R 再平方数值上面是一样的。^[3]

R平方：决定系数，反应因变量的全部变异能通过回归关系被自变量解释的比例。\(R^2\) 值越接近1，吻合程度越高，越接近0，则吻合程度越低。\(R^2\) 作为相关系数，一般机器默认的是\(R^2\) >0.99，这样才具有可行度和线性关系。^[4]

Jay's Blog

皮尔森（逊）相关系数（Pearson Correlation Coefficient, PCC）

摘要

皮尔森相关系数

线性回归的R平方

参考文献