随机森林填充空值

导入各自包：

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
# from sklearn.datasets import load_boston  # 新版本无波士顿数据
from sklearn.impute import SimpleImputer  # 填充缺失值的类
from sklearn.ensemble import RandomForestRegressor  # 随机森林回归
from sklearn.model_selection import cross_val_score  # 交叉验证

1 波士顿数据集获取

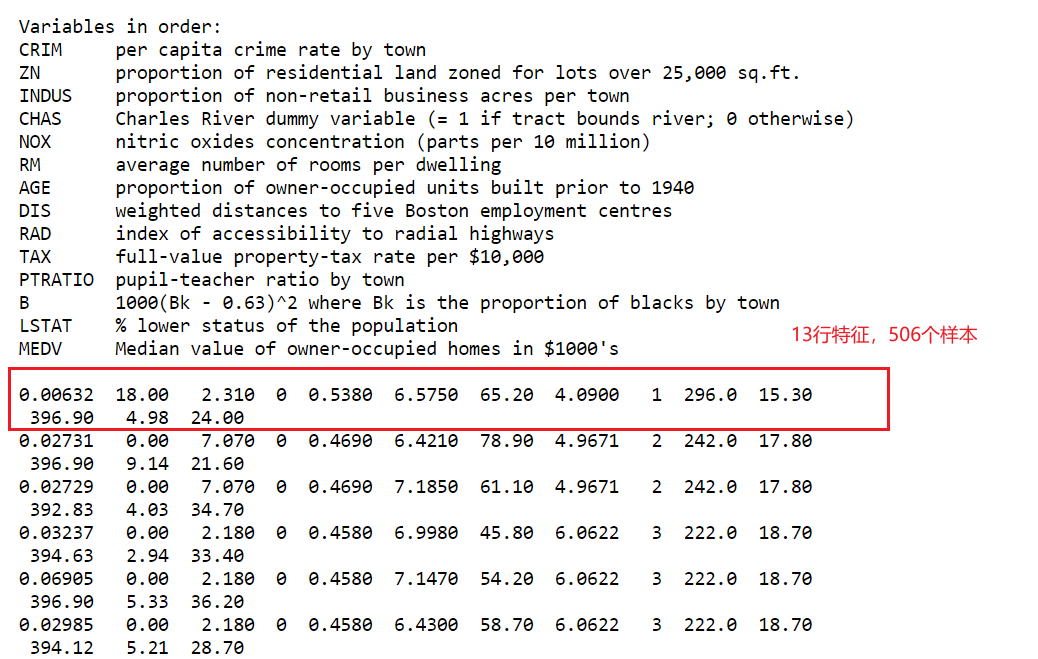
利用犯罪率、是否邻近查尔斯河、公路可达性等信息，来预测 20 世纪 70 年代波士顿地区房屋价格的中位数。这个数据集包含 506 个数据点和 13 个特征。波士顿房价数据集在scikit-learn1.2版本以后被移除了,通过其他网站获取，该数据已整理成excel,放置于：https://github.com/sdhlw/OA/tree/main/Boston_data

数据：前12行为特征即x，最后一行为y

data_url = "http://lib.stat.cmu.edu/datasets/boston"
raw_df = pd.read_csv(data_url, sep="\s+", skiprows=22, header=None)
data = np.hstack([raw_df.values[::2, :], raw_df.values[1::2, :2]])
target = raw_df.values[1::2, 2] # 归一化和特征构造后都没有变化
print("Data shape: {}".format(data.shape))

2 设置缺失样本

rng = np.random.RandomState(0)  # 确定随机种子
missing_rate = 0.5   # 缺失率是50%
# 计算缺失的样本总数；floor是向下取整
n_missing_samples = int(np.floor(n_samples * n_features * missing_rate))  # 行乘列乘0.5即取一半缺失值
print(n_missing_samples)  # 3289 个数

1
2
3

# randint(下限,上限,n)：在上限和下限之间随机取出n个整数
missing_features = rng.randint(0, n_features, n_missing_samples) # (0,13,3289)
missing_samples = rng.randint(0, n_samples, n_missing_samples) # (0,506,3289)

X_missing = X_full.copy()
y_missing = y_full.copy()
X_missing[missing_samples,missing_features] = np.nan  # 指定为nan，代表缺失掉的数据
# y_missing 不变
X_missing = pd.D

3 数据填充

3.1 均值填充

1
2
3

imp_mean = SimpleImputer(missing_values=np.nan, strategy="mean")  # 指定缺失值是什么和用什么填充
X_missing_mean = imp_mean.fit_transform(X_missing)  # fit + predict---->特殊接口transform
pd.DataFrame(X_missing_mean).isnull().sum() # X_missing_mean是一个ndaraay

3.2 0值填充

1
2
3

imp_0 = SimpleImputer(missing_values=np.nan, strategy="constant", fill_value=0)   # 用0进行填充
X_missing_0 = imp_0.fit_transform(X_missing)
pd.DataFrame(X_missing_0).isnull().sum()

3.3 随机森林填充

假设一个具有n个特征的数据，特征T存在缺失值（大量缺失更适合），把T当做是标签，其他的n-1个特征和原来的数据看作是新的特征矩阵，具体数据解释为：

数据	说明
Xtrain	特征T不缺失的值对应的n-1个特征+原始标签
ytrain	特征T不缺失的值
Xtest	特征T缺失的值对应的n-1个特征+原始标签
ytest	特征T缺失值（未知）

注意：如果其他特征也存在缺失值，遍历所有的特征，从缺失值最少的开始。

缺失值越少，所需要的准确信息也越少
填补一个特征，先将其他特征值的缺失值用0代替，这样每次循环一次，有缺失值的特征便会减少一个

假设数据有n个特征，m行数据：

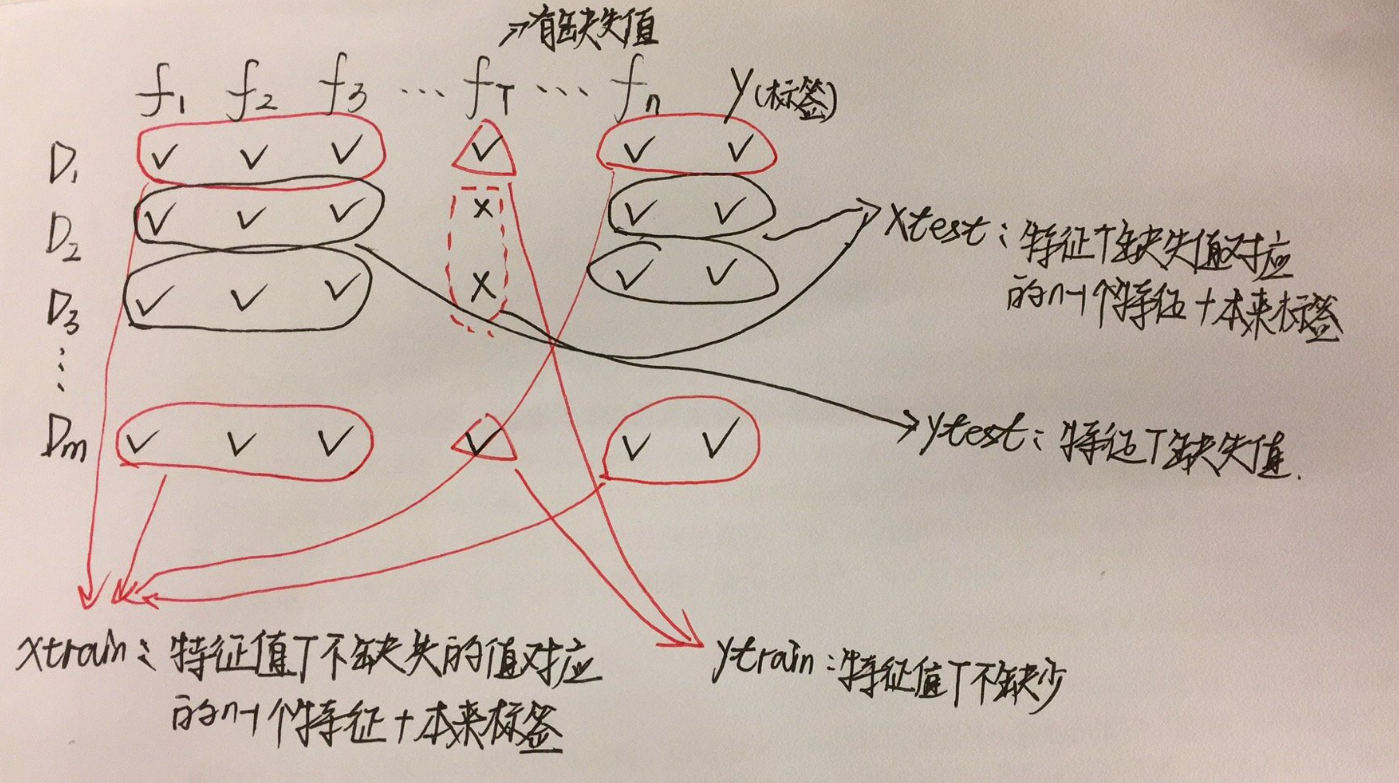
由于是从最少的缺失值特征开始填充，那么需要找出存在缺失值的索引的顺序：argsort函数的使用

1
2
3

X_missing_reg = X_missing.copy()
# 找出缺失值从小到大对应的索引值
sortindex = np.argsort(pd.DataFrame(X_missing_reg).isnull().sum(axis=0)).values

填充过程：

for i in sortindex:
    # 构建新的特征矩阵和新标签
    df = X_missing_reg   # 所有的操作都在df上进行，只是最后得到的填充值作用在X_missing_reg上面
    fillc = df.iloc[:, i]   # 某个需要填充的列，索引为i

    # 没有被选中填充（!=）的特征与原始标签的连接起来；df就是新特征矩阵
    df = pd.concat([df.iloc[:, df.columns != i], pd.DataFrame(y_full)], axis=1)

    # 新的特征矩阵df中，对含有缺失值的列，进行0的填补
    # 检查是否有0 pd.DataFrame(df_0).isnull().sum()
    df_0 = SimpleImputer(missing_values=np.nan, strategy='constant', fill_value=0).fit_transform(df)

    # 找出训练集和测试集
    ytrain = fillc[fillc.notnull()]  # 被选中填充的特征矩阵T中的非空值
    ytest = fillc[fillc.isnull()]  # 被选中填充的特征矩阵T中的空值
    Xtrain = df_0[ytrain.index, :]  # 新特征矩阵上，被选出来要填充的特征的非空值对应的记录
    Xtest = df_0[ytest.index, :]   # 空值对应的记录

    # 随机森林填充缺失值
    rfc = RandomForestRegressor(n_estimators=100)
    rfc = rfc.fit(Xtrain, ytrain)
    y_predict = rfc.predict(Xtest)  # predict接口预测得到的结果就是用来填充空值的那些值
    # 将填补好的特征返回到我们的原始特征矩阵中
    X_missing_reg.loc[X_missing_reg.iloc[:, i].isnull(), i] = y_predict

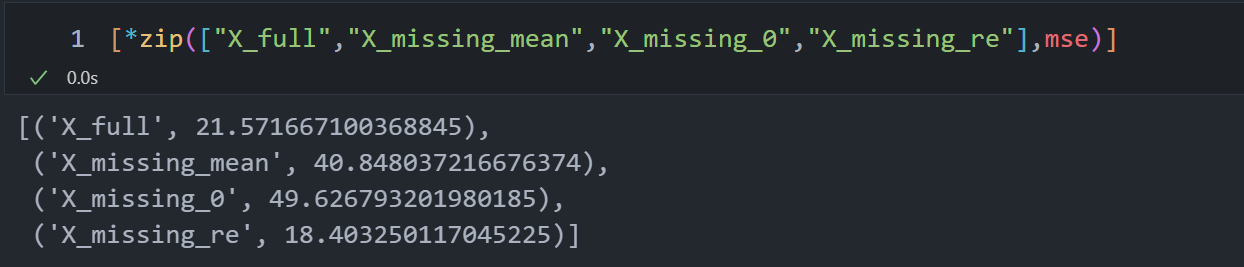
4 四种数据建模

MSE：均方误差；回归树的衡量指标，越小越好。sklearn中使用的是负均方误差neg_mean_squared_error。均方误差本身是种误差loss，通过负数表示
R2：回归树score返回的真实值是R的平方，不是MSE

X = [X_full, X_missing_mean, X_missing_0, X_missing_reg]
mse = []

for x in X:
    estimator = RandomForestRegressor(random_state=0, n_estimators=100)
    scores = cross_val_score(estimator, x, y_full, scoring="neg_mean_squared_error", cv=5).mean()
    mse.append(scores * -1)

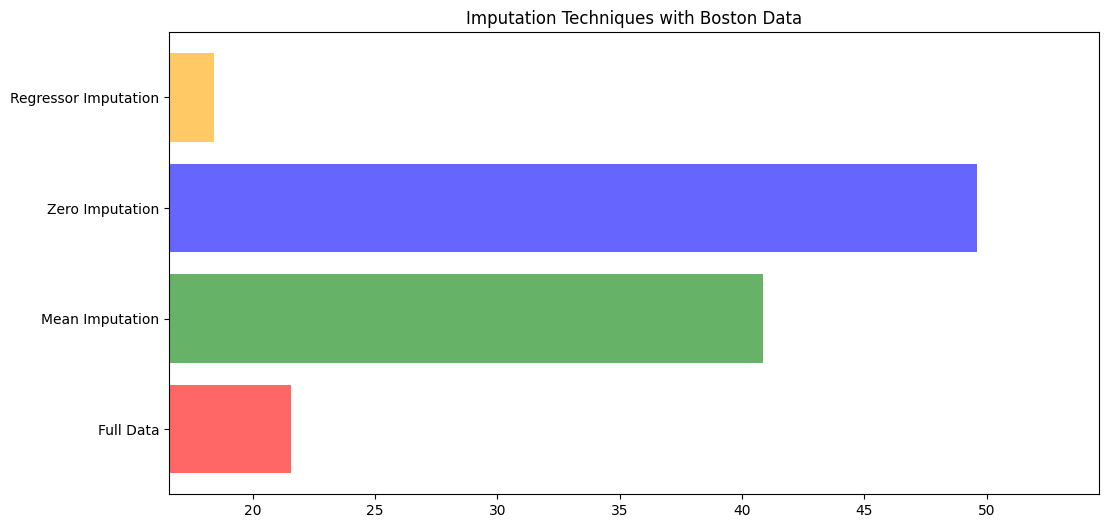
5 绘图

x_labels = ["Full Data",
           "Mean Imputation",
           "Zero Imputation",
           "Regressor Imputation"]

colors = ['r', 'g', 'b', 'orange']

plt.figure(figsize=(12,6))  # 生成画布
ax = plt.subplot(111)  # 添加子图

# 在上面的过程中已经求出了4种不同数据的MSE
for i in np.arange(len(mse)):  # arange(4)
    ax.barh(i, mse[i], color=colors[i],alpha=0.6,align='center')

ax.set_title("Imputation Techniques with Boston Data")  # 标题
ax.set_xlim(left=np.min(mse)*0.9,
           right=np.max(mse)*1.1)  # 横轴是mse的取值

ax.set_yticks(np.arange(len(mse)))
ax.set_label("MSE")
ax.set_yticklabels(x_labels)   # 用x_labels中的名字作为y轴的命名
plt.show()

参考文章

无